Random Physics Note (Feb 12)
- Michelle Dong
- Feb 12, 2022
- 9 min read
Helicity & Chirality
Helicity is a quantum number.
If you have photonic states with different helicity (quantum number), then they are clearly different quantum states so they for all purposes are different particles.
In 4 spacetime dimensions, you can deduce that there is only 3 values of helicity -1, 0, 1.
But, the funny thing is, the helicity is identified under spatial inversions/parity transformations and thus the -1 and 1 are identified.
So even though naively, there might be 2 quantum states that WOULD'VE been two different kinds of electromagnetic photos. Parity identifies them to be the same photon.
However, if you have a parity violating term. You could argue that there are more than one type of photons.
---
Something similar actually comes up with the quantum number called chirality.
For all practical purposes, nearly everything is charged under the chirality quantum number.
Chirality is the eigenvalue under the (gamma 5 dirac matrix).
It turns out that chirality decomposes your Hilbert space in exactly half to those spinors that have +1 chirality or -1 chirality.
So, we say that particles can either be left handed or right handed.
Electromagnetic and gravitational forces preserve this chirality.
So all the left handed and right handed particles we identify as the same thing.
Even though for e.g. the electron has chirality, there is only "1" electron.
But the electroweak interaction breaks chirality. It does not preserve chirality.
So suddenly, you will find that you really do have a new particle. Left handed electrons are NOT the same as right handed electrons.
And the electroweak interaction only affects left handed electrons.
[After reading Weinberg 2.5, the more complicated ideas would be talked.]
Quantum Field Theory?
Quantum field theory is not the way it is because it's trying to make special relativity consistent with quantum mechanics.
There are examples of non-relativistic quantum field theories.
Quantum field theory is just quantum mechanics applied to fields.
However, if you have a quantum mechanical system that obeys the special relativity (has Lorentz symmetry), then it must be a quantum field theory.
No... that's also not true. Lol.
In conclusion... just be careful when people make those statements.
Polyakov action is an example of a quantum mechanical system that obeys special relativity in flat space.
It is not a quantum field theory, it is a string theory.
Anyhow ... Quantum field theory is quantum mechanics on fields. That's it.
And relativistic spin does arise from special relativity... But there are notions of spin that are completely independent of relativity. For example, isospin.
Non-existing Particles, aka. Vacuum
Non-existing particles particles are literally just called the vacuum.
So, there is a rigorous way of formulating a Lorentz invariant vacuum.
Strangely enough ... Wonder if non-equilibrium systems ... which somehow break time reversal symmetry and lack a vacuum are actually breaking Lorentz symmetry.
A non-existing particle is the state on a Hilbert space that has non-four momentum whatsoever.
It is still mathematically consistent in relativistic quantum mechanics.
But this state that has no four momentum.
Four momentum = (hamiltonian, spatial momentum)
[My class says Four momentum = (energy, spatial momentum)
Hamiltonian for all practical purposes is energy, but strictly speaking it's the Hamiltonian.]
But also, that state that has no momentum, is the same thing as saying that state really has no energy, no momentum... So what is it? If it has no other quantum numbers to characterize it, then it is the state of non-existence.
Hence, what a non-existing particle naively but it's really just vacuum.
What does it mean for something to physically exist?
And the conclusion was that, at the very minimum, it must be able to exchange energy and momentum. Exchange being the key term.
So, strangely enough, the vacuum may have zero energy and momentum... Can it exchange something?
What does it mean to exchange? Can it be excited?
To be excited, means to obtain momentum and energy.
To excite the vacuum means to create a particle.
So the vacuum even though it is a "state of nonexistence naively" is a physical thing. Because it can exchange energy and momentum.
There are deeper questions to ask later.
One of the things is:
The vacuum depends on the Hamiltonian/Lagrangian that you define your theory with.
So if you have a free theory (no interactions), the you have what's known as the free vacuum (usually called the vacuum).
But if you have an interacting theory, then you get an interacting vacuum.
In 233A, when we start introducing interaction terms into the Lagrangian, the gphi^3 for example, that will change the vacuum of an equilibrium theory to an interacting vacuum.
Grassmann Algebra
Grassmann algebra i.e. the algebra of non-commuting numbers.
[For fermionic path intergrals]
Grassmann numbers are a new kind of number system.
But they work very similar.
The only difference is the following:
If a, b are both Grassmann numbers, then ab = -ba (anti-commutative)
One of the first things you can deduce is a^2 = 0.
And what you should know is that from the underlying numbers, we can construct function on Grassmann numbers, theories of differentiation, everything that we usually do in algebra, analysis, and topology.
Integration is exactly equivalent to differentiation on Grassmann numbers.

(Wikipedia)
Supernumber = regular real number + Grassmann number
In other words, a super number has a part that is commutative and a part that is anticommutative.
And the generalization of analysis, topology, geometry is just super- in front.
Superanalysis,
supergeometry,
supermanifolds,
supertopology.
Tensor Calculus
Tensor Order & Perturbative Order

(Wikipedia)


(Andres)
Supersymmetry
N labels the number of supersymmetries.
Introducing N=2 supersymmetry creates fancy new physics in even the simplest Quantum Mechanics Models.
In fact, so much that it constrains the hamiltonian to be positive definite. So it gets rid of potentials like -1/r that would be seen for hydrogen atom.
But introducing N=4 supersymmetry constrains the quantum mechanical system so much more further that now the potential function can also only be holomorphic. And holomorphic functions from complex analysis are so so so so so so heavily constrained. That it can only be polynomials. No other functions. They're the nicest functions.
The more supersymmetries that you introduce into a theory, the more constrained the theory becomes and a result, even more solvable as the possible Lagrangians/Hamiltonians become so constrained and simple.
But at some point, you over-constrain your system by adding to many supersymmetries. So there could be a maximal supersymmetry that you can impose, before you break the entire thing.
So supersymmetric theories can become so crazily constrained that it just deletes theories.
Spinors


There are 3 types of fermions that need to be familiar with.
Dirac, Weyl, and Majorana all refer to different types of spinor representations.
Anomalous Quantum Theory

Anomalous quantum theory cannot be quantized.
These are related to the supergravity anomalies, gravitational anomalies, gauge anomalies, etc.
QCD is going to have a gauge anomaly.
String Theory in fact has an anomaly that must be eliminated.
The conformal anomaly: it turns out eliminating this anomaly is what ells you how many dimensions the theory exists in.
Super conformal field theory is equivalent Calabi-Yau manifolds.
***
When studying differential geometry, topology, etc., things feel formulated.
When studying conformal field theories, you will see that these are just examples of quantum generalizations of classical geometry (classical meaning like diff. geo, topology).
So when you talk about conformal field theories, you are really considering things called quantum geometry (quantum manifolds and so forth).
Conformal field theories give several generalizations of the math.
***
Matrix Method

This is probably the most legitimate method but it is such a pain.
A Question
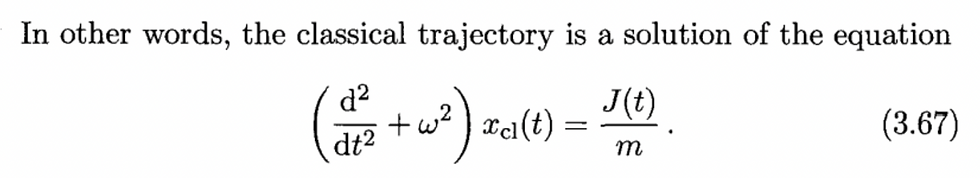
(The ODE itself does't make sense so need to randomly make an i epsilon prescriptions.)
Poincare Group
The poincare group is characterized by its invariants under Lorentz transformations which are the hamiltonian and square of the four momentum.
They are characterized by the possible signs.
It must therefore be noticed that the physically plausible representations of the little group be those that correspond to massive and massless representations (where the massive in string theory could be complex valued but not necessarily physical).
Then after you've characterized the massless and massive representations, you can choose to ask whether or not you are considering a representation where the reference momentum is timelike, spacelike, or lightlike.
In the case of the momentum being x-like, you must also determine whether or not the class of momentum that you are considering is future or past oriented.
The light cone is indeed in the tangent space.
Commutative Operator
Two operators commute iff there exist a simultaneous eigenbasis of those oeprators.
It is the reason why we can even label states in quantum mechanics.
Complex Analysis
Heat Kernels and Dirac Operators
Nicole Berline, Ezra Getzler, & Michèle Vergne, Heat Kernels and Dirac Operators
Instantons and large N
Marcos Mariño, "Instantons and large N: An introduction to non-perturbative methods in QFT"
When Hamiltonian Equals to Energy
It is always equal to the energy but it may not necessarily be what you would call the "energy" due to the particle itself.
For example, if you consider the Hamiltonian of a particle just moving with linear momentum p. H = p^2/2m. Then you consider a change of charts (coordinate system) in such a way that the particle appears to be accelerating. Then H will get a new term due to the accelerated reference frame. H = p^2/2m + something complicated. That something complicated, you might claim it is no longer part of the energy. But something that you could attribute to the fact that you're in an accelerated reference frame. Then a lot of people might say, the Hamiltonian is no longer the energy.
When Would You Use Lagrangian/Hamitonian
This just depends on the problem.
It also depends on what kind of physicist you would ask. The thing about Lagrangians is that it's very easy to implement gauge symmetries into Lagrangians, but not Hamiltonians.
Hamiltonians are not gauge invariant and as you saw just now, they are not even invariant under coordinate system change of charts.
You change the chart, the Hamiltonian changes. It is not a diffeomorphism invariant.
But people like Lagrangians, they are diffeomorphism invariants. And they are singlets under more complicated gauge symmetry groups.
The Lagrangian is a singlet. You can show that it must be a singlet/scalar quantity. So it is easy to write down what terms are in it by constraining them all be singlets.
To get to know how to show that Lagrangian is a singlet, the Quantum Gauge Theories needed to be known (can check out Quantization of Gauge Systems by Hennaeux and Teitboim.
For 105 Classical Mechanics, there is absolutely almost zero reason to use one over the other. The reason is really only there for HEPT.
If you do the path integral properly (derivation, properly). You will notice that what pops out is NOT the Lagrangian. You don't actually get exp(i integral L). You get exp (i integral (pq - H)) where p is some momentum conjugate to the generalized coordinate q, and H is the Hamiltonian. You have to path intergrate over all conjugate momenta to obtain the Lagrangian.
The result being:
This seems an argument for the Hamiltonian in fact being more fundament.
This is known as the hamiltonian path integral but the issue is that... It's just not invariant under transformations. So it is really annoying to deal with,.
We need to consult the specialized book to do it more justice.
The other thing that's a bit more useful is:
For upper divs and maybe engineering applications:
Lagrangian formalism when you use it, you use the Euler-Lagrangian Equations, there are second order equations if your system doesn't have anything crazy (like higher order derivatives in the Lagrangian density). Second order PDEs/ODEs are much harder to solve than first order. In the Hamiltonian formalism, you actually get first order equations. So that's one reason for using the Hamiltonian, but it's really just good for numerics.
The Hamiltonian is what pops up when you try to quantize >>PARTICLES<< via the Schrodinger Equation and/or it is relativistic generalizations like the dirac equation for a particle.
The Hamiltonian is also technically what allows you to create ensembles in statistical mechanics, statistical field theories. In fact, even if you try to create a thermal quantum field theory, what you will see is that the first step is finding the partition function as usual. Z = Tr(exp(-beta H)) where H is the Hamiltonian and beta is coldness. And this trace is interpreted once again as the Hamiltonian path integral.
Hamiltonian seems to be more fundamental but it is annoying to deal with. It is not a singlet.
The singlet object that is supposed to actually represent energy and momentum with diffeomorphism invariance. The one that makes sense to calculate is what we know as the Stress Energy Momentum Tensor.
Stress Energy Momentum Tensor is a second rank symmetric tensor that is divergentless meaning that it's conserved. If T is the tensor and D is the covariant derivate, it satisfies D T = 0.
What we interpret as the Hamiltonian is in fact the 00 component of the stress tensor. T_00 = H.
Maybe the question is ill-defined to begin with. Because what defines a physical theory is the observables you can measure. Expected values.
And you can get these without any path integral, using symmetry only as we talked about before.
Not to mention, there is probably around 100+ generalization of the Hamiltonians/Lagrangians/different mechanics that people have developed over the years. But they're just used in extremely niche applications.
It is just that the Lagrangian and Hamiltonian formalism of mechanics has been very fruitful and is mainstream. Not just in physics but also in mathematics.
Like this paper, Sato Mechanics:

What's probably better to say is:
What mathematical objects should one study for a classical mechanics framework?
The answer lies deeply in symplectic geometry and it is generalizations like Poisson geometry and so forth.
But the answer physically is still. A mathematical space to describe the system (generally called phase space), a set of observables that you can measure, and some way to time evolve everything (symplectic form).
Phase Space
Phase space at the most basic level for classical mechanics is literally just the cartesian product of all possible positions with all possible momentums.
Let X be phase space X = {(x, p), where x is all positions of the particle, p is all momentums of particle} for Physics 105.
Phase space would have a whole new meaning when learning more.
Derivatives
Lie Derivative
Frechet Derivative
Covariant Derivative
Exterior Derivative
Variational Derivative
Schwarzian Derivative
Gauge Covariant Derivative
Exterior Covariant Derivative
Total Exterior Covariant Derivative
Super Gauge Covariant Derivative
Super Lie Derivatives
Graded Derivatives
Fractal Derivatives
Holomorphic Derivative
Anti-holomorphic Derivative
Quaternoic Derivative
Spinor Derivatives
Spinor Covariant Derivatives
Material Derivatives
Hodge Dual Derivatives
and many more perhaps...
And all their generalizations to divergences, laplacians...
In functional analysis, there is several notions of derivatives one can define based off the underlying topological space.










Comments